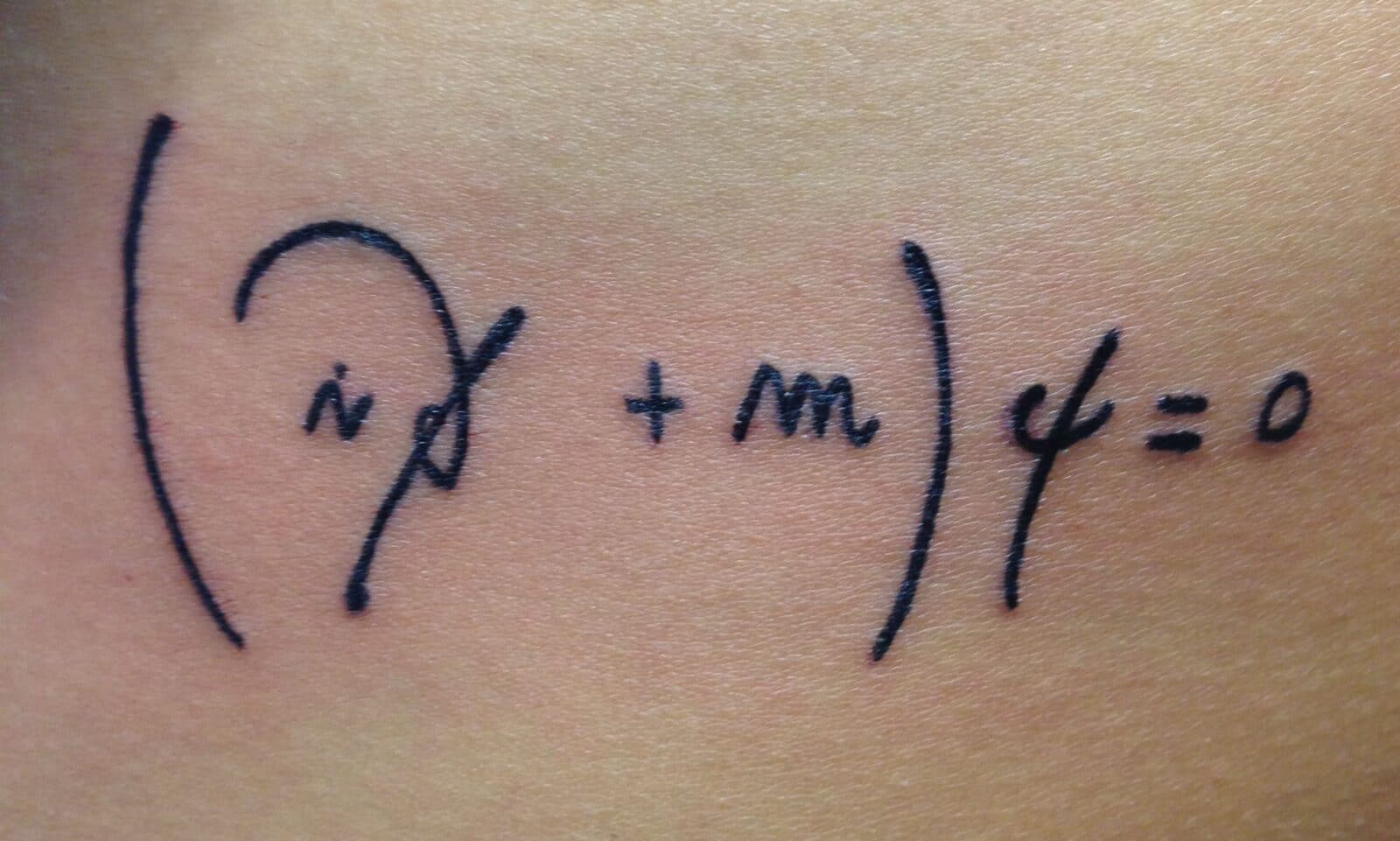L’equazione di Dirac, simbolo di inguaribili romantici

Alzi la mano chi almeno una volta nella vita ha sentito parlare dell’equazione di Dirac. È vero, la maggior parte di coloro che leggono ora sono con le mani alzate, cercando di ricordare dove e in quali circostanze hanno incontrato questa equazione. E se, invece dell’equazione di Dirac, ti dicessimo “amore equazione“? Riesci a pensare a qualcosa di più specifico?

L’equazione di Dirac come poesia romantica

Molti di voi conoscono l’equazione di Dirac come amore equazione, e quindi come la più romantica delle equazioni fisiche. Fidanzate e innamorate sono ammaliate da questa equazione, che spesso si ritrova tatuata su avambracci e polsi, a testimonianza del legame indissolubile tra i due Romeo e Giulietta.

Come si può vedere dal tatuaggio, l’equazione è riportata come $$ ( partial + m) psi = 0. $$ L’interpretazione romantica deriva da questa definizione di sistemi fisici “entangled”:

Se due sistemi interagiscono tra loro per un certo periodo di tempo e vengono poi separati, non possiamo più descriverli come due sistemi separati, ma in qualche modo diventare sottilmente un sistema.

Quello che succede a uno di loro continua a influenzare l’altro, anche se sono lontani anni luce.

È chiaro che la definizione di entanglement quantistico si presta facilmente a interpretazioni più shakespeariane e più morbide. Se mettiamo in relazione questo concetto con l’equazione di Dirac e affermiamo che esprime lo stesso concetto, come nelle migliori fiabe, una fredda equazione fisico-matematica può diventare un potente simbolo d’amore. Ma è un peccato che non sia così.

La teoria della relatività speciale: punto di partenza dell’equazione di Dirac

Per capire perché l’equazione di Dirac non ha nulla a che fare con la passione di due amanti, bisogna coglierne il significato più profondo e, per quanto possibile, la derivazione matematica.

Nel 1905 Albert Einstein formulò la teoria della relatività speciale. Come molti di voi sanno, descrive la cinematica e la dinamica di corpi massicci che si muovono quasi alla velocità della luce. In poche parole, è un file generalizzazione della fisica newtoniana, con la modifica del cosiddetto invarianti fisiche, ovvero le quantità che restano fisse anche al variare del sistema di riferimento da cui sono considerate.

Einstein ha mostrato che nella relatività ristretta, ilinvariante relativistico dinamico coinvolge l’energia cinetica e quantità di moto secondo la relazione $$ E ^ 2 – p ^ 2 c ^ 2 = m ^ 2 c ^ 4, $$ dove (E ) rappresenta l’energia cinetica, (p ) la quantità di moto, (m ) la massa dell’oggetto e (c ) la velocità della luce. L’equazione afferma che, l’energia e la quantità di moto fisse di un oggetto, la massa è obbligata a rispettare la suddetta legge.

Quantificazione ed equazione di Klein-Gordon

L’equazione di Klein-Gordon rappresenta il primo tentativo di fondere la meccanica quantistica e la relatività speciale. Partendo dalla relazione di invarianza relativistica, introduciamo la costante di Planck normalizzata ( non h ) e la funzione d’onda ( psi ), che descrive lo stato quantistico di una particella elementare. Il modulo quadrato di ( psi ) non è altro che la funzione di densità di probabilità, che ci dice la probabilità che una particella si trovi in ​​una certa area dello spazio-tempo.

Riscrivendo energia e quantità di moto secondo complesse operazioni matematiche, che qui omettiamo, arriviamo all’equazione di Klein-Gordon $$ ( partial_ mu partial ^ mu – dfrac {m ^ 2 c ^ 2} { non h ^ 2}) psi = 0. $$ Il problema era che le soluzioni a questa equazione potevano portare a probabilità negative., che matematicamente non ha senso, poiché la probabilità è una misura compresa tra 0 e 1.

L’equazione di Dirac

Nel 1928, il fisico Paul Dirac ha deciso di andare oltre i limiti dell’equazione di Klein-Gordon e scrisse una legge che rispettava i principi matematici di calcolo delle probabilità. In un colpo di genio, ha definito un’espressione lineare di energia, senza estrarre la radice quadrata della formula di invarianza relativistica: $$ E = alpha pc + mc ^ 2 beta $$ dove ( alpha ) e ( beta ) sono array definiti correttamente (4 volte 4 ). Quantificando questa espressione lineare, dopo complesse manipolazioni matematiche, arriviamo all’equazione $$ (i gamma ^ mu dfrac { partial} { partial x ^ mu} – m) psi = 0, $ $ dove ( mu = 0,1,2,3 ) rappresenta l’indice per muoversi nelle quattro dimensioni dello spazio-tempo. Ora, per renderlo più compatto, di solito definiamo ( not partial = gamma ^ mu dfrac { partial} { partial x ^ mu} ), arriviamo all’equazione di Dirac come la conosciamo oggi, ovvero: $$ (i not partial – m) psi = 0. $$

Il vero significato dell’equazione di Dirac

Come suggerito dalla dimensione degli array ( alpha ) e ( beta ), L’equazione di Dirac è in realtà un sistema di quattro equazioni, cioè, la funzione d’onda ( psi (x, t) ) è un vettore quadridimensionale. Da un punto di vista puramente matematico, l’equazione di Dirac è un’equazione differenziale per derivate parziali, con funzione d’onda sconosciuta. Se al contrario entriamo nel mondo della fisica, dove questa equazione vive davvero, possiamo dirlo descrive il movimento dei fermioni in modo relativista invariante. Questi ultimi sono particelle di spin semi-intere, come elettroni, protoni e quark.

L’equazione di Dirac risolve quindi il problema delle probabilità negative, ma continua ad ammettere soluzioni energetiche negative. Lo stesso Dirac non aveva una spiegazione fisica precisa del motivo per cui ciò fosse accaduto.e ha ipotizzato l’esistenza di un mare di buchi di energia negativa formati spostando i fermioni in uno stato eccitato. In realtà questa spiegazione è stata rifiutata dalla comunità scientifica, e finalmente il paradosso dell’energia negativa è stato spiegato pochi anni dopo, con la scoperta del positrone.

Perché l’equazione dell’amore è solo un’invenzione romantica

Come forse avrai già notato, l’equazione dell’amore e l’equazione di Dirac sono molto diverse. In quest’ultimo, la derivata è tagliata, è premoltiplicata dall’unità immaginaria e la massa ha un segno meno. A peggiorare le cose, L’equazione di Dirac descrive il moto di una particella libera, cioè non interagisce con campi esterni (come campi magnetici o gravitazionali) o con altre particelle. In una parola, L’equazione di Dirac ci racconta la storia delle particelle solitarie e isolate, ma ardenti amanti!

Proprio per questo motivo L’equazione di Dirac non ha nulla a che fare con il concetto di entanglement quantistico: è associato alle proprietà matematiche degli spazi di Hilbert, cioè a oggetti misteriosi in cui vivono e prendono forma gli stati quantistici di due particelle. E se ancora non sei convinto pensa questo fenomeno di “interlacciamento” si verifica solo a livello microscopico, cioè quando è opportuno introdurre la quantizzazione.

Così inguaribili romantici, non farti tatuare l’equazione di Dirac, perché se lo fai, è come dire alla tua dolce metà che vuoi continuare il viaggio … da solo!